Envoie moi le fichier , mais au passage , tu n'as pas besoin d'excel.Une calculatrice te suffit pour me donner tes résultats.
je veux voir tes résultats ici sur ton topic merci.
Non, non, le sujet sera clos et tu pourras vérifier que les 2 méthodes sont équivalentes (que la seconde est bien une alternative à la première !!)
Voici le fichier:
http://www.fichier-xls.fr/2013/01/06/hx738ar/
Mais puisque tu veux aussi les résultats en direct, les voici:
Pour ta variable (nombre de sorties)
La variance par lancer est 0.02629657 (aussi bien avec ta définition qu'avec la mienne).
L'écart-type est donc 0.162162162 par lancer
L'écart-type est donc 6 pour 1369 lancers
(Une nouvelle fois, rien à voir avec la variance et l'écart-type du sujet !)
Envoie moi le fichier , mais au passage , tu n'as pas besoin d'excel.Une calculatrice te suffit pour me donner tes résultats.
je veux voir tes résultats ici sur ton topic merci.Non, non, le sujet sera clos et tu pourras vérifier que les 2 méthodes sont équivalentes (que la seconde est bien une alternative à la première !!)
Voici le fichier:
http://www.fichier-xls.fr/2013/01/06/bj45v1p/
Mais puisque tu veux aussi les résultats en direct, les voici:
Pour ta variable (nombre de sorties)
La variance par lancer est 0.02629657 (aussi bien avec ta définition qu'avec la mienne).
L'écart-type est donc 0.162162162 par lancer
L'écart-type est donc 6 pour 1369 lancers(Une nouvelle fois, rien à voir avec la variance et l'écart-type du sujet !)
Donc tu trouves 0,02629657 *1369 = 36 pour la variance
et 0,162162162*1369 = 221,999... pour ET
pour ma part , variance = (30-37)² = 49
donc ecart-type = 7
à remarquer que l'ET est toujours inferieur à la variance puisque c'est la racine carrée , 0.162162162 par lancer est donc faux.
Tes résultats sont faux , sujet clos pour moi.
Donc tu trouves 0,02629657 *1369 = 36 pour la variance
Oui
et 0,162162162*1369 = 221,999... pour ET
Non, l'écart-type est la racine carrée de la variance, donc l'écart-type est 6 comme annoncé.
Il ne faut pas multiplier par 1369 mais par 37 et 0.162162162 *37 = 6
L'écart-type n'est pas proportionnel au nombre de lancers mais à la racine carrée du nombre de lancers
pour ma part , variance = (30-37)² = 49
donc ecart-type = 7
Nous ne sommes donc pas d'accord en effet.
à remarquer que l'ET est toujours inferieur à la variance puisque c'est la racine carrée , 0.162162162 par lancer est donc faux.
Faux, la racine carrée d'un nombre compris entre 0 et 1 est plus grande que ce nombre lui-même.
Par exemple la racine carrée de 0.25 est 0.5. La racine carrée est plus grande que le nombre lui-même
Tes résultats sont faux , sujet clos pour moi.
Quelle façon de conclure !
En résumé, tu auras dit à tort que:
j’avais trouvé des variances négatives
ma définition de variance était fausse
la preuve était (a-b)²=....
la racine d’un nombre était forcément plus petite que le nombre
l’écart type pour 1369 lancers était 1369 plus grand que l’écart-type par lancer
mes résultats étaient faux
l'écart-type était 7 ( probablement à cause d'un échantillon dont on a rien à foutre: le zéro sorti 30 fois au lieu de 37 ?)
Et tout cela au sujet d'une variable aléatoire qui n'était même pas celle de mon sujet. Chapeau !
Qu'est-ce que vous essayez de démonter ?
Que vous êtes l'un comme l'autre aussi nul !
Qu'est-ce que vous essayez de démonter ?
Que vous êtes l'un comme l'autre aussi nul !
Il ne manquait plus que celui-là !
Et qu'il ramène surtout sa fraise de cette façon-là !
Parfois ton humour dépasse le mien glups , j'en suis jaloux
Non, je ne crois pas.
Et puis tu vois, nous n'arrivons pas à la cheville d'Artemus24 et de Picsous !
Ok, ce n'est pas la même catégorie, ni le même registre !
La formule du calcul de la variance est donnée par 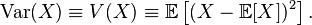
Le X représente la variable aléatoire.
Posons comme les valeurs suivantes, de cette variable aléatoire :
--> 0 si le résultat de la roulette n'est pas le zéro.
--> 1 si le résultat de la roulette est le zéro.
Picsou dit qu'en 1369 (=37*37), il y a eu seulement 30 sorties du zéro; nous retiendrons donc cette hypothèse de calcul.
On obtient 30 fois le 1 et 1339 (=1369-30) fois le 0. On trouve comme moyenne : E(X) = 30/1369.
(si au lieu de 30 fois, nous avions eu 37 alors E(X) = 37/1369, c'est-à-dire 1/37, ce qui est conforme au jeu de la roulette).
Ensuite le calcul des écarts, en valeur absolue, donne :
--> pour le 0, on a : (0 - 30/1369)^2 = (30/1369)^2
--> pour le 1, on a : (1 - 30/1369)^2 = (1339/1369)^2
Le calcul de la variance donne :
--> [ (30/1.369)^2 * 1339 + (1.339/1.369)^2 * 30 ] / 1.369
--> [ (900 * 1.339 + 1.792.921 * 30) / 1.874.161 ] / 1.369
--> [ (1.205.100 + 53.787.630) / 1.874.161 ] / 1.369
--> [ 54.992.730 / 1.874.161 ] / 1.369
--> [ 29,3425858290 ] / 1.369
--> 0,02143359081
L'écart-type donne : 0,1464021544152878
On est loin de vos résultats !
@+
L'écart-type donne : 0,14604021544
Tu veux dire 0.146402154415288?
On est loin de vos résultats !
Nous sommes surtout loin de parler de la même chose.
******************************************************************************************************************************************************************************
Mais comme tu sais maintenant utiliser autre chose que la formule de la loi binomiale, je reprends ta définition de variance qui est si chère également à Picsous.
J'en profite pour recalculer la variance de la roulette pour un numéro plein et retrouver le résultat de mon premier message de ce sujet que tu as toujours dénié.
La formule du calcul de la variance est donnée par 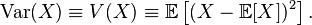
X représente la variable aléatoire.
Posons comme les valeurs suivantes, de cette variable aléatoire :
--> 35 si le résultat de la roulette est le numéro que nous avons joué.
--> -1 si le résultat de la roulette n'est pas le numéro que nous avons joué.
On reconnaît la variable aléatoire du gain
La probabilité de gagner étant 1/37 et celle de perdre 36/37, on trouve comme moyenne : E(X) = -1/37.
Ensuite le calcul des écarts, en valeur absolue, donne :
--> pour le 35, on a : (1296/37)
--> pour le -1, on a : (36/37)
Le calcul de la variance donne :
--> [ (1296/37)^2 + (36/37)^2 * 36 ] / 37
--> V(X) = 34.08035 environ
Comme le dit Picsou, tu confonds Espérance Mathématique avec Moyenne.
Comme le dit Picsou, tu confonds Espérance Mathématique avec Moyenne.
Oui, bien sûr... Où ça ?
Picsous a aussi dit que mes calculs avaient donné des variances négatives.
Picsous a aussi dit que la racine carrée d'un nombre ne pouvait pas être plus grande que ce nombre etc, etc...
E(X) désigne une moyenne et non l'espérance mathématique.
Ma variable que j'ai définit est constitué que de 0 et de 1, et cela sur 37 * 37 coups, soit 1369.
Si il y a que 30 sorties pour le 1, la moyenne est :
--> (30 * 1 + 1339 * 0) / 1369.
--> 30 / 1369.
Pourquoi trouves-tu -1/37 ?
@+
E(X) désigne une moyenne et non l'espérance mathématique.
Quand on utilise la lettre E, c'est généralement pour parler de l'espérance.
C'est la lettre consacrée comme v pour la vitesse, t pour le temps et x pour une inconnue.
Pourquoi trouves-tu -1/37 ?
Parce que je ne parle pas de la série statistique constituée de 1369 nombres (avec 30 uns et 1339 zéros).
Quand je parlais à Picsous, je me moquais de son échantillon.
Il n'y a pas besoin d'échantillon pour calculer l'espérance. (Je ne me suis donc pas servi de 30)
Quand je trouve -1/37, je parle de la roulette en général. Je ne parle pas ni de Picsous, ni d'un échantillon.
Je parle à nouveau de mon sujet initial :
ça ne t'a pas échappé que l'espérance à la roulette est -1/37 ?
D'accord pour l'espérance mathématique.
Mais alors, ce n'est pas la bonne formule pour calculer la variance. Car si tu ne veux pas introduire ni le nombre de coups, ni les résultats obtenus par les résultats, je ne vois pas comment calculer cette variance.
Car si tu ne veux pas introduire ni le nombre de coups, ni les résultats obtenus par les résultats, je ne vois pas comment calculer cette variance.
Grâce à la définition "Artemus/Picsous" par exemple ou grâce à la définition que j'ai utilisée (elles sont équivalentes).
Tu n'as pas besoin du nombre de coups car ces définitions te donnent le résultat par lancer.
Il est alors facile ensuite d'avoir le résultat pour, par exemple, 1369 lancers (Pas une série particulière où il y aurait 30 zéros par exemple mais une "série moyenne")
Tu ne vois pas comment ?
Mais il suffit de lire:
Je viens de donner le développement du calcul avec ta définition et j'avais donné celui (beaucoup plus détaillé) avec ma définition lors du premier message de ce sujet.
Les 2 formules montrent que lorsqu'on mise sur un numéro, l'espérance est -1/37 avec une variance de 46256/1369 (par lancer)
Bonsoir,
Je viens de surfer sur ce topic, ou le sujet est de calculer une certaine espérance, de calculer certaines probabilités en fonction d'un écarts type, bon... soit...
Comment calculer l'espérance de sortie du 1 par rapport à celle du 36 ? .... en faisant des moyennes ?
AMHA, il n'y a pas de possibilité dans cette direction.
Si, si... peut être ?, mais faudrait-il réduire chaque nombre à son plus petit dénominateur commun, ce qui n'est pas le cas dans la logique présentée, mais bon à chacun ses idées.
Comment attribuer une juste valeur à un numéro, doit t-on vraiment lui attribuer la valeur de 5 si c'est le numéro 5, la valeur de 33, si c'est le numéro 33 ?
Il y a à boire et à manger à ce sujet...
Que l'on me parle de la loi du tiers oui, de celle des grands nombres, oui, de celle des petits nombres, oui...
L'écart type n'est à mon sens sens issue d'aucune véritable loi en matière de roulette... l'écart type permet de faire des statistiques, mais de ne permet pas de faire ou de construire certaines probabilités.
Crldt
